5week] Balanced Search Trees

2-3 Search Trees

균형 탐색트리로 자식노드를 2, 3개를 가지고 있는 형태를 가진다.

• 2-node : 1개의 key, 2개의 자식노드
• 3-node : 2개의 key, 3개의 자식노드

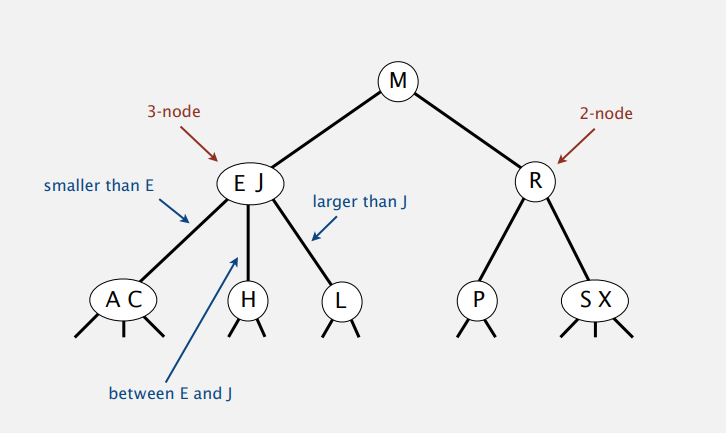
예제에서 보듯 기본 BST와 같이 정렬되어 트리를 구성한다.

특징 : root→leaf(null link)까지의 거리가 모두 같아 완벽한 균형을 이룬다.

Search

1. 2-node
   1. key보다 작으면 → left 자식
   2. key보다 크면 → right 자식
2. 3-node
   1. 두 key보다 작으면 → left 자식
   2. 두 key의 사이면 → middle 자식
   3. 두 key보다 크면 → right 자식

Insert

1. 삽입할 target node가 2-node일 때
   1. 3-node로 교체
2. 삽입할 target node가 3-node일 때
   1. 임의의 4-node 로 교체 ( key가 3개 ) → 이 때 잠시 2-3 Search Tree가 성립하지 않는다.
   2. 4-node의 key 값의 중간 값을 부모 노드에 추가하고 자식노드를 2-node로 교체 ( 재귀적으로 )
   3. root 임시로 4-node가 된다면, 1-2)를 거치며 전체의 length가 1 증가한다.

 

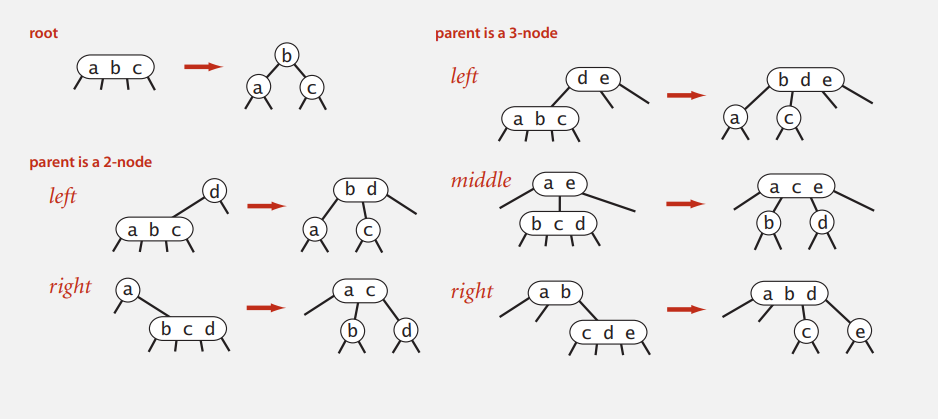
insert가 되는 다양한 예시 그림

2-3 Tree 구현은 따로 안하고, R-B Tree에서 구현을 한다. ( 기존 BST 에서 몇 줄만 추가되는 정도 )

Left-leaning Red-Black BSTs ( R-B Tree )

위에서 배운 2-3 Tree를 BST로 나타낸다 . ( 색깔을 나르게 나타내는 방법 사용 )

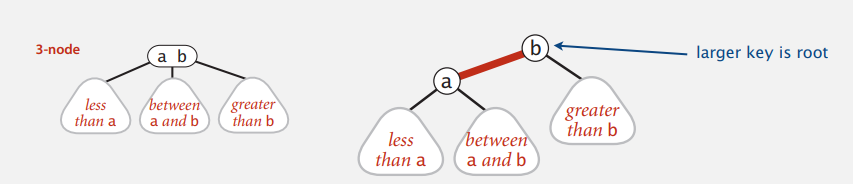
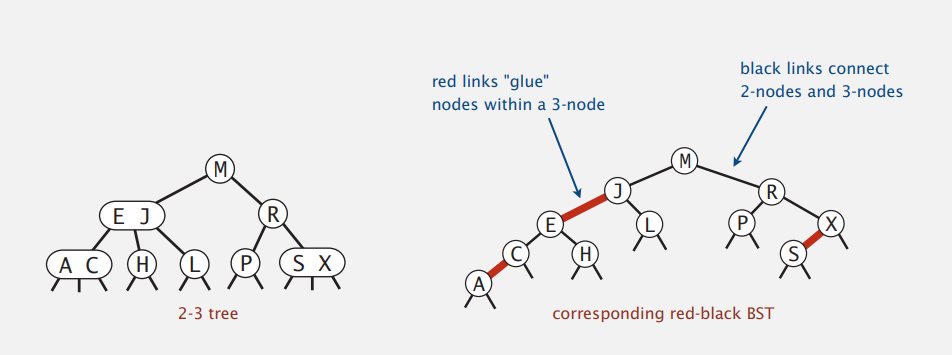
R-B Tree의 규칙

1. Red 가 겹쳐지는 노드는 존재하지 않음.
2. Red Node는 왼쪽으로 기울어짐
3. Root→Leaf 까지 Black Node의 개수가 모두 같음 ( 완벽한 균형 )

2-3 Tree 와 R-B Tree의 1:1 mapping

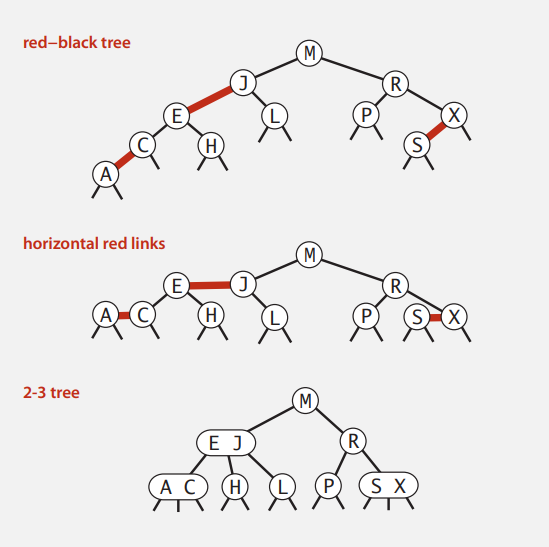
기존 BST의 연산은 그대로 사용 가능하다. ( search, floor, iteration, selection )

public Val get(Key key)
{
	 Node x = root;
	 while (x != null)
	 {
			int cmp = key.compareTo(x.key);
			if (cmp < 0) x = x.left;
			else if (cmp > 0) x = x.right;
			else if (cmp == 0) return x.val;
	 }
	 return null;
}

 

구현 코드에 color 관련 내용이 없음.

 

초기화 코드의 경우 color의 내용이 추가된다.

 

private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node
{
	Key key;
  Value val;
  Node left, right;
  boolean color; // color of parent link
}
private boolean isRed(Node x)
{
  if (x == null) return false;
  return x.color == RED;
}

R-B Tree의 경우 총 3가지의 추가되는 기본 연산 3가지가 존재한다.

1. left-rotation
2. right-rotation
3. color-flip

Left-rotation

• 오른쪽으로 치우친 Red link를 왼쪽으로 바꿔주는 연산( 조건 : 왼쪽 자식은 Black이고, 오른쪽 자식이 Red 일 때 )

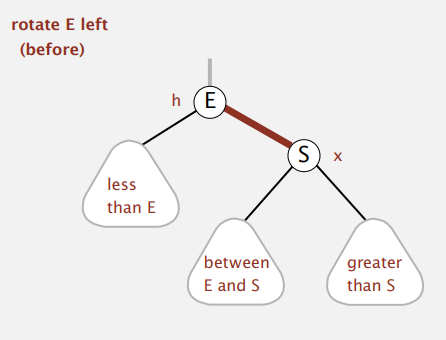
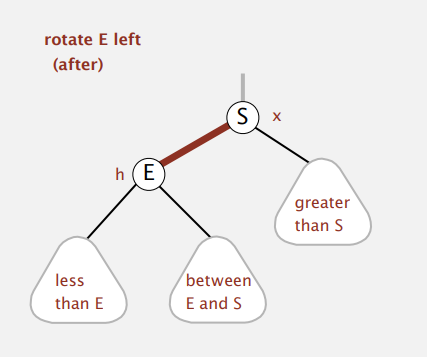
private Node rotateLeft(Node h)
{
	 assert isRed(h.right);
	 Node x = h.right;
	 h.right = x.left;
	 x.left = h;
	 x.color = h.color;
	 h.color = RED;
	 return x;
}

Right-rotation

• 왼쪽으로 치우친 Red link를 오른쪽으로 바꿔주는 연산( 왼쪽의 자식 & 왼쪽 자식의 왼쪽 자식이 Red 일 때 )

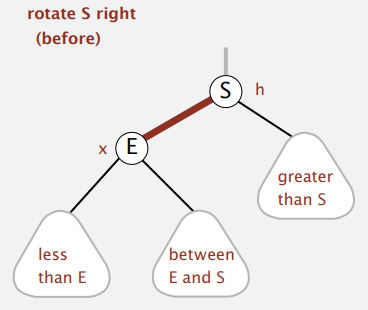
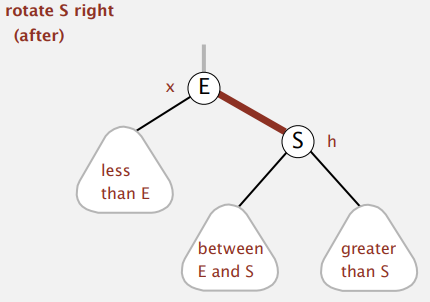
private Node rotateRight(Node h)
{
	 assert isRed(h.left);
	 Node x = h.left;
	 h.left = x.right;
	 x.right = h;
	 x.color = h.color;
	 h.color = RED;
	 return x;
}

Color-filp

• 임시로 4-node가 되었을 때 색을 바꿔주는 연산( 자신은 Black이고 모든 자식이 Red 일 때 )

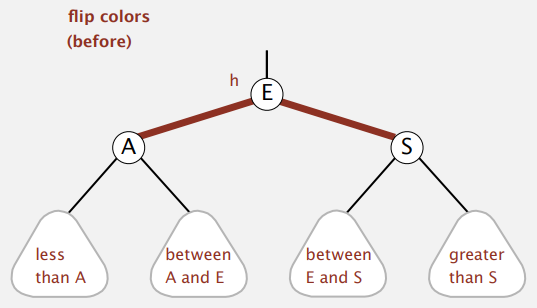
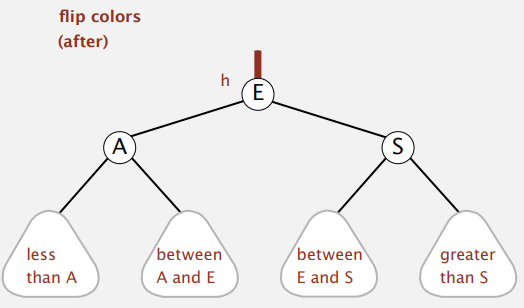
private void flipColors(Node h)
{
	 assert !isRed(h);
	 assert isRed(h.left);
	 assert isRed(h.right);
	 h.color = RED;
	 h.left.color = BLACK;
	 h.right.color = BLACK;
}

위의 3가지 연산을 통해 R-B Tree가 유지 되며 기본 전략은 위의 설명과 같이

2-3 Tree 와 1:1 mapping하는 전략

Case 1 : 2-node 에 삽입 ( 자식에 Red Node가 없는 경우 )

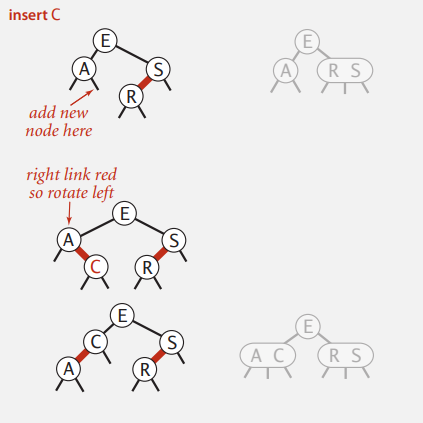
Case 2: 3-node 에 삽입 ( 이미 자식에 Red Node가 있는 경우 )

Case 2-1 : 반복할 필요 없는 경우

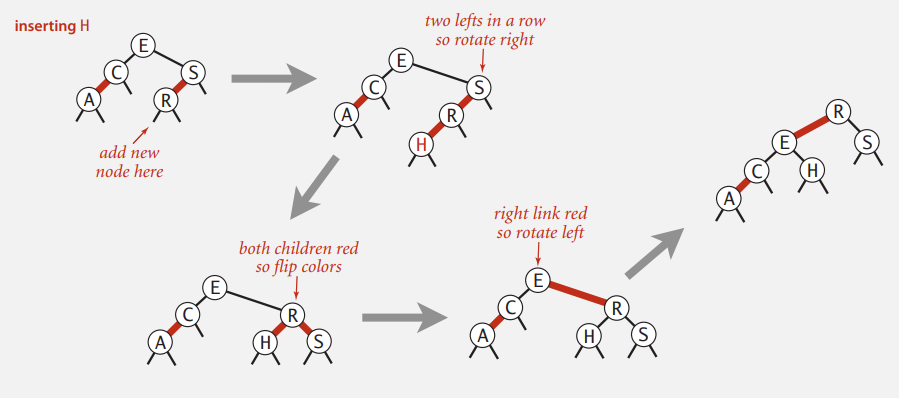
Case 2-2: 반복이 필요한 경우

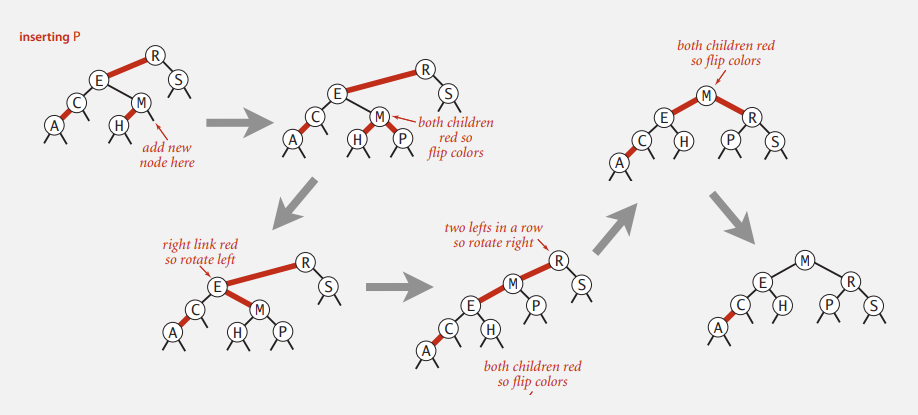
이 모든 Case 를 같은 코드에서 처리하도록 만들어야함. ( insert )

private Node put(Node h, Key key, Value val)
{
	 if (h == null) return new Node(key, val, RED);
	 int cmp = key.compareTo(h.key);
	 if (cmp < 0) h.left = put(h.left, key, val);
	 else if (cmp > 0) h.right = put(h.right, key, val);
	 else if (cmp == 0) h.val = val;
	 if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
	 if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
	 if (isRed(h.left) && isRed(h.right)) flipColors(h);

	 return h;
}

R-B Tree는 균형있는 Tree가 만들어지며, 검색 속도가 안정적